On using operations research to plan social dinners

In this post, I share how I helped organize social dinner events using combinatorial optimization, open data, and static website generators. Over the last five years, I planned routes for hundreds of students participating in events hosted in Munich by Academy Consult and later also from CDTM and Manage & More. A changing group of students from those organizations (my friend Max Walther being one of the constants) organized these events. I was lucky enough to be part of both as a planner and participant, and I wanted to thank all of them for making it happen. Their dedication made it an unforgettable experience! This post will focus on my technological contribution to those events. I will first introduce the concept of a running dinner, then elaborate on the operational considerations, present the user interface, and conclude with how good travel time data can be computed using open data. I will publish the source code of the optimization model and frontend builder in the near future.

What is a running dinner?

A running dinner¹ (alternatively flying dinner, progressive dinner, safari supper) is a social dinner event where each course of a multi-course dinner is hosted by one of the participants in their kitchen. Participants are assigned to teams that each cook and host a single course and, in turn, visit other teams so that a full dinner is assembled throughout the evening. For example, a team assigned the Entreé prepares that meal and hosts two other teams. The team will then be a guest at a different team that hosts a main course and travel to a final team that hosts a desert. As every team prepares and serves their course within their own kitchen, teams are constantly “running” between courses. There is usually a central afterparty, where all teams meet and conclude the evening. In the following, I will use a running dinner format with teams of two and a total of three courses as examples.

Figure 2 above shows an illustration of an optimal route assignment focussing on Team A. Team A starts in their own kitchen and is joined for the first course by Team B and C. After the course, each team continues to a different kitchen, with Team A heading for the Kitchen of Team D. Teams B and C leave for two different kitchens, their routes are only partially sketched. Team A, Team D, and Team E, arrive for the second course that Team D hosts. Team A then heads on to the Kitchen of Team F, and then on to the afterparty. Note that given the illustrated assignment of Team A, both Teams B and C are not allowed to join for the final course served by Team F as they then would meet with Team A twice, which is not allowed. The example only shows the very limited view of Team A. In practice, there could be more than 30 teams that all need to be scheduled to synchronize with each other while ensuring that tours remain short.

Assignment and Routing Considerations

The running dinner forms an interesting combinatorial optimization problem with several real-world constraints:

The most fundamental constraint is that every team hosts exactly one course and is then a guest for the two other courses. This means that the total number of teams must be divisible by 3, the number of courses, and that each course is hosted by 1/3 of the total number of teams. Since a running dinner is a social event, we want to maximize the number of unique connections between people; the teams should, therefore, only meet once over the course of the entire event. Further, to stay in the spirit of “running,” we also enforce a minimal travel time of a few minutes, such that if kitchens of multiple teams are located within the same building, e.g., in a student dormitory, we do not travel purely between them. Sometimes, not enough participants can offer their kitchen, so we admit multiple teams in the same kitchen. In this case, we must ensure that the teams cook different courses. For each team, we record the travel time for the entire event. We generally assume that teams prepare their dishes in their kitchen prior to the first course and that all teams visit the afterparty, and thus include the travel time from the team’s first kitchen to the assigned first course and the travel time from the assigned last course to the afterparty location.

Given these constraints, we want to optimize the assignment for: i) the participants’ preferences to host specific courses and, ii) the time spent traveling between courses and to the afterparty. For travel time, we want to consider both global welfare (minimizing the sum of total time traveled) and individual fairness (reducing the maximum time traveled by a single team).

User Experience Considerations

Participants must be well supported before and during the event.

We assume that signing up for the event is done through existing channels of the community, and that an event organizer collects personal information, kitchen addresses, and course preferences, and then groups participants into teams based on personal preferences, kitchen availability, and dietary preferences. We then need to communicate to participants which team they are a part of, share contact information, and announce the course the team is hosting. Further, it is essential to share the names of the guests and any potential allergies or dietary restrictions.

During (and in preparation for) the event, participants must be given information on which other teams must be visited, how they can best reach that location, and when they must leave the previous course to arrive on time. Such travel-time information should be as accurate as possible to make sure that each course can start on time.

Assignment and Route optimization

I have used a mixed integer linear programming formulation for the problem. Depending on the problem size, a pure (meta)heuristic solution might be more advisable. The model is an extension of “Rudi Linear Solver” (2016) by Michael Timpelan. Input data is fed to the model as a CSV file, and results are written to a JSON file. The JSON file is then used to render the web frontend. I initially coded the model using Gurobi’s gurobipy model but then switched to a generic implementation using the PuLP library that is compatible with a wide variety of open source and commercial solvers.

We define $\mathcal{T}$ as set of teams, $\mathcal{C} = 0..2$ as a set of courses, and $\mathcal{G} = 0..(|T|\div|C|)$, as the set of groups (number of parallel hosts). The set $\mathcal{B}$ contains tuples $(i,j)$ for those teams $i,j \in\mathcal{T}$ that share a kitchen and thus must not be assigned to the same course. We use a travel-time matrix $d_{ij}$, describing the travel time between the kitchen of team $i\in \mathcal{T}$, to the kitchen of any other team or the afterparty $j\in \mathcal{T}\cup\{'a'\}$. For our objective function, we define the parameter $\alpha$ to weight the total travel time, the parameter $\beta$ to weigh the maximum individual travel time, and the parameter $\gamma$ to weigh the chef preference assignment. The parameter $p_{tc}$ states the preference of team $t\in\mathcal{T}$ to cook course $c\in\mathcal{C}$. Its values should be normalized such that it is compatible with objective functions weights $\alpha$, $\beta$,and $\gamma$. We define a binary variable $v_{tgc}$ that indicates if team $t\in\mathcal{T}$ is assigned to group $g\in\mathcal{G}$ for course $c\in\mathcal{C}$, ($v_{tgc}=1$), or not ($v_{tgc}=0$). We then define a binary variable $c_{tgc}$ which indicates if team $t\in\mathcal{T}$ is the chef for group $g\in\mathcal{G}$ in course $c\in\mathcal{C}$, ($c_{tgc}=1$), or not ($c_{tgc}=0$). . We add binary arc variable $a_{cijtg}$ that indicates if team $t\in\mathcal{T}$ travels between the kitchens of team $i\in\mathcal{T}$ and team $j\in\mathcal{T}$ to reach the course $c\in\mathcal{C}$, ($a_{cijtg}=1$), or not ($a_{cijtg}=0$). To increase the fairness of an assignment, we further add a variable $d^{\max}$ that will be used to identify and limit the largest time a team travels for all three courses.

Our assignment problem then reads as follows:

The objective function consists of three terms, each weighted with a custom factor. The total travel time is calculated using all taken movement arcs. For flows to the last course, we further account for leaving that course for the afterparty.

$$\begin{array}{lrl} &\text{preferences} = & \sum_{t\in\mathcal{T}, g\in\mathcal{G}, c\in\mathcal{C}} c_{tgc} p_{tc} \\[4pt] &\text{total-time} = & \sum_{c\in\mathcal{C}, (i,j,t)\in\mathcal{T}^3, g\in\mathcal{G}} a_{cijtg} d_{ij} + \sum_{(i,j,t)\in\mathcal{T}^3, g\in\mathcal{G}} a_{|C|ijtg} d_{j,'a'} \\[4pt] \text{minimize} & z = & \alpha \cdot \text{total-time} + \beta \cdot d^{\max} - \gamma \cdot \text{preferences} \\ \end{array}$$

We add the following constraints to the minimization problem:

We ensure that each team is participating in exactly one group per course and that for each group and course, the total number of assigned teams is equal to the number of courses (i.e., if the dinner has three courses, three teams meet at each course):

$$\begin{array}{lll} \sum_{g\in\mathcal{G}} v_{tgc} &= 1 &\ \forall t\in\mathcal{T}, c\in\mathcal{C} \\ \sum_{t\in\mathcal{T}} v_{tgc} &= |\mathcal{C}| &\ \forall g\in\mathcal{G}, c\in\mathcal{C} \end{array}$$

We then ensure that teams can only meet once using overlapping set constraints. If two teams have met in $g_1$ for a course (the first summand is 2), then they must not be both assigned to the same group $g_2$ at a later course (the second summand then also being 2, making the total 4, which would violate the constraint ).

$$(v_{t_1g_1c_1} + v_{t_2g_1c_1}) + (v_{t_1g_2c_2} + v_{t_2g_2c_2}) \leq 3 \ \forall c_1\in\mathcal{C}, c_2=c_1..|\mathcal{C}|, (g_1,g_2)\in\mathcal{G}^2, t_1\in\mathcal{T},t_2=t_1..|\mathcal{T}|$$

Every group and course must have one team assigned as chef, and every team is chef only once:

$$\begin{array}{lll} \sum_{t\in\mathcal{T}} c_{tgc} &= 1 &\ \forall g\in\mathcal{G}, c\in\mathcal{C} \\ \sum_{g\in\mathcal{G}, c\in\mathcal{C}} c_{tgc} &= 1 &\ \forall t\in\mathcal{T} \end{array}$$

A team can only be the chef for a course and group if it is assigned to that group and course. A team must only have movement flows to courses and groups when it is assigned to them.

$$\begin{array}{lll} c_{tgc} &\leq v_{tgc} &\ \forall t\in\mathcal{T}, g\in\mathcal{G}, c\in\mathcal{C} \\ \sum_{i\in\mathcal{T},j\in\mathcal{T}} a_{cijtg} &\leq v_{tgc} &\ \forall t\in\mathcal{T}, g\in\mathcal{G}, c\in\mathcal{C} \end{array}$$

For those teams in $(i,j)\in\mathcal{B}$ that share a kitchen, we must ensure that they do not cook the same course.

$$\sum_{g\in\mathcal{G}} (c_{igc} + c_{jgc}) \leq 1,\ \forall (i,j)\in\mathcal{B}, c\in\mathcal{C}$$

Each team must have a movement flow from their kitchen to the first course. A movement arc to team $t$ for course $c$ can only exist if $t$ is the chef for course $c$.

$$\begin{array}{lll} \sum_{j\in\mathcal{T}} a_{0tjtg} &\leq v_{tg0} &\ \forall t\in\mathcal{T}, g\in\mathcal{G} \\ a_{ctjtg} &\leq c_{jgc} &\ \forall c\in\mathcal{C}, g\in\mathcal{G}, (i,j,t)\in\mathcal{T}^3 \\ \end{array}$$

We enforce flow preservation on the movement arcs between courses $c-1$ and $c$, i.e., there can only be an outgoing flow if there is an incoming flow.

$$\sum_{j\in\mathcal{T}|i \neq j,g\in\mathcal{G}} a_{cijtg} = \sum_{r\in\mathcal{T},g\in\mathcal{G}} a_{(c-1)ritg} \ \forall c=1..|\mathcal{C}|,t\in\mathcal{T}, i\in\mathcal{T}$$

We then ensure that the maximum team travel time variable is at least as high as every team’s aggregated travel time and that arcs with a travel time of zero are forbidden to take.

$$\begin{array}{lll} \sum_{c\in\mathcal{C}, (i,)\in\mathcal{T}^2, g\in\mathcal{G}} a_{cijtg} &\leq d^{\max} &\ \forall t\in\mathcal{T} \\ \sum_{} a_{cijtg} & = 0 &\ \forall c\in\mathcal{C}, (i,j) \in\mathcal{T}^2 |\ d_{ij} = 0, t\in\mathcal{T}, g\in\mathcal{G}\\ \end{array}$$

Frontend design

With the routes and teams assigned, this decision must now be communicated to all participants. I decided to do so with a single static website that contains pages for every team team. The organizing team can then decide whether to send deep links to individual team pages or to share a single index page. I initially used ElderJS, then Astro as a frontend builder. Both take a JSON data set as input (the output of the assignment problem) and allow us to use modern web technologies to create static HTML files. A minimal amount of Java Script is included to rewrite the address links to launch the user’s platform default application (Google Maps for Android, Apple Maps for iOS, DuckDuckGo for Desktop) in routing mode, as support for the generic “geo:” handler is unfortunately flaky. I used no CSS framework and coded the design using minimal modern and responsive CSS.

Each team page features the same basic layout: Each course is represented as a block that contains information about the course, the desired arrival time, information about the guests or host, allergy and dietary restrictions, and information about the teams’ address and estimated travel time. Clicking the address link auto-launches the device’s default routing application.

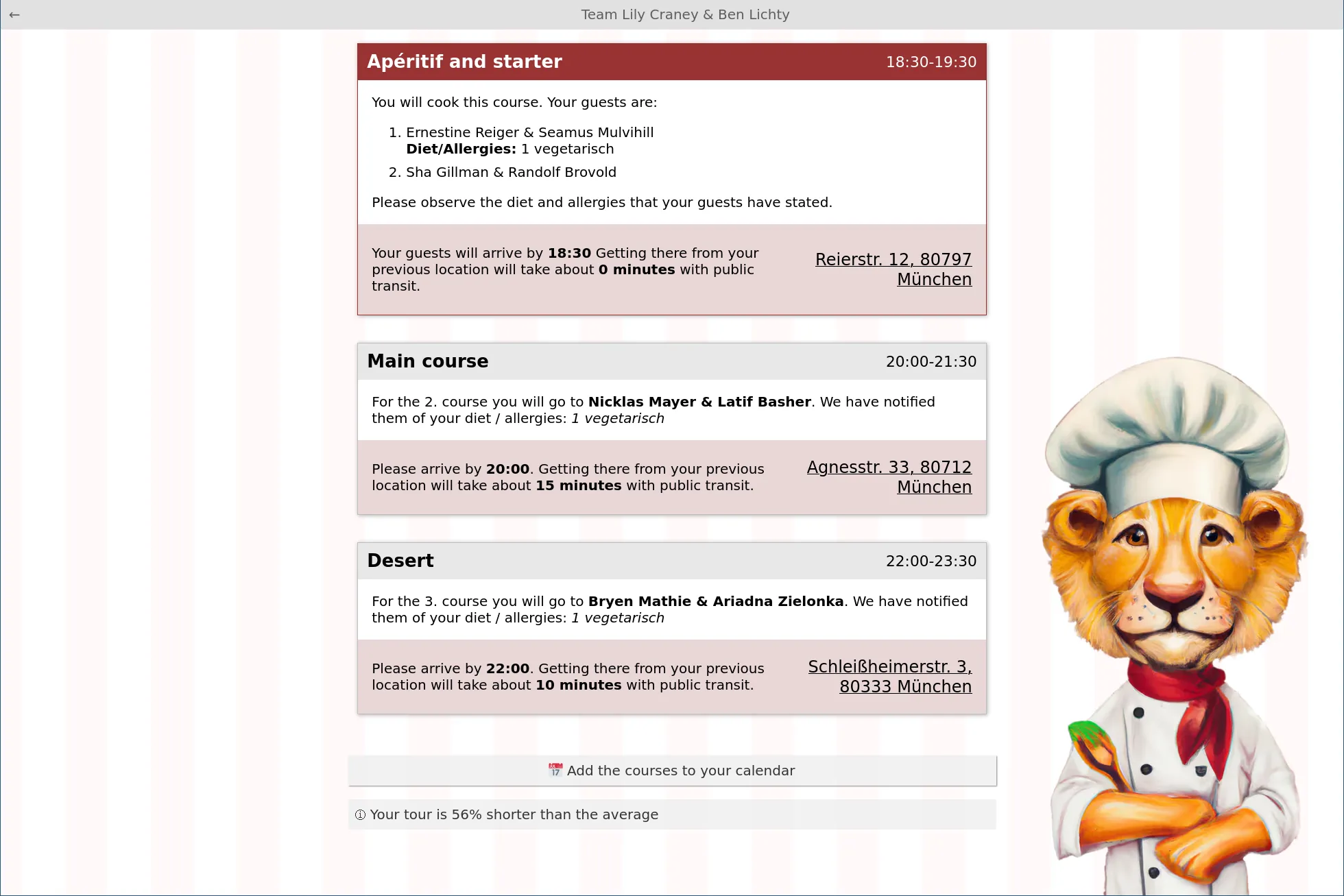
The block’s colors and the background image can then be quickly themed to match any theme of the event. Figure 4 below shows the website with a Camping/Outdoor theme. I used the color scheme of the US National Park Service and used DALL E to generate an Image of a lion (Academy Consult’s mascot) in a ranger uniform and a chef’s hat.

To further increase the usability, I create an ICS calendar file for each team, containing the assigned courses, including all meta information. A participant who added this ICS file to their calendar can thus forgo using the web application entirely during the event. On some operating systems, the calendar application will launch a reminder based on live travel time data for the addresses stored.

Accurate Travel Time Data

The travel time calculation has been the component with the highest amount of churn within the project. Simply using the Euclidian distance between coordinates becomes very inaccurate when considering different modes of transportation. Initially, the code was a single-file Python script, which I later refactored to use a more organized structure with multiple possible endpoint implementations. Public transport data was initially sourced from 3rd party web services, which were not very stable. I finally found a great solution based only on open-source software and data by combining OpenStreetMaps road network data, GTFS Transit Feeds, and the Motis and OSRM routing engines. In the following section, I quickly introduce the different attempts.

1. Mvg-api (3rd party)

The first event was held in winter, and I assumed that participants would take public transport. Luckily, someone had made mvg-api, an unofficial Python module for the local transport company, that allows for querying the travel time between two points. Each request hits the official web service and thus needs to be rate-limited quite heavily to stay within usage limits. Since the module uses an undocumented internal API, it was relatively unstable but workable. Unfortunately, after some time, internal API changes made this solution unfeasible.

2. OSRM (Local)

The next event was held in the summer; thus, I assumed that most participants would use their bikes. This also allowed us to set up the open-source routing engine OSRM on OpenStreetMaps data. I already had experience of using OSRM for my PhD project. Using the bike profile allows for very accurate estimates. OpenStreetMap Data © OpenStreetMap contributors was used under the Open Database License ODbL.

3. HAFAS (3rd party)

Unfortunately, the mvg-api stopped working after some time as the transport company’s API changes broke the module. As a quick fix, I replaced it with pyhafas, which uses an API from Germany’s federal train company instead. Again, I had to use a very strict rate-limiting scheme.

4. Motis Project (Local)

In the final iteration, I switched evaluation to a local Motis project server. The Motis open-source project combines the car, bike, and foot navigation capabilities of the OSRM project with a custom routing algorithm for public transport in a unified multi-mode routing engine. As required by EU regulation 2017/1926, transport companies must make their stops and schedules available in a machine-readable format (standardized on NeTEx and the more popular GTFS). The Motis project engine then takes this information to include it in their multi-modal routing. For our setting, I only allow the bike, foot, and public transport modes and choose the fastest available for our travel time estimate.

Using the Motis project with open data locally is the best option, matching the quality of the 3rd party route services with the performance and independence allowed by local computation. As rate limiting was not an issue anymore, I could now afford to query the routing engine with the specific times of the course, i.e., create a distinct travel-time matrix for every course. Due to the superiority of this method, I will likely remove all other options and refactor the code back to a compact single-file Python script.

Future Work

Currently, the team assignment is out of the scope of the assignment problem. If most participants can offer their kitchen to host, including a kitchen selection within the optimization model would be very interesting. Participants with a well-located kitchen could then host and be paired with the remaining participants.

I have supervised two Bachelor’s theses about the running dinner problem: Daniel Nientiedt has written his Bachelor’s thesis, “Design of an Algorithm for Planing and Assigning Guests in a Running Dinner Event While Minimizing Travel Distances” (2018), on extending the shown model to include more extensive consideration of team preferences. Veronika Eisgruber wrote her thesis, “Developing a Heuristic to Solve the Running Dinner Problem for a Large Number of Participants” (2019), on how to solve the problem more efficiently using heuristics. When attempting to rewrite the optimization shown above, their ideas should be considered.

Footnotes

1. “Running dinner” is used descriptively for this kind of social dinner event as defined in the Wikipedia article. No relation to or affiliation with any of the trademarks in this area. ↩